Interesting stuff.. how to approximately calculate 11^8 quickly without a calculator

You guessed it.. Taylor series...

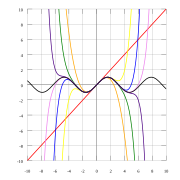
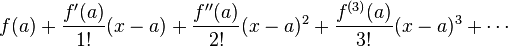HEre's the taylor series for f(x+ ) .
It is a simple expansion series of any function around a small increment .

Where are higher order terms (greater than the power of three). If we ignore
the higher order terms as well as the third order term then we can write:

And in the limiting case when we have

If you carefully look at the above equation then we will see a striking resemblance
to the famous Ito's stochastic equation, which is the basis of Black-Scholes option
pricing partial differential equation (PDE). The only difference is that in Ito's
equation we have the term instead of , that is in an Ito process we have

The above equivalence has a great intuitive meaning with respect of geometric Brownian motion and asset price movement, but that is not the purpose of this article. What we wanted to show was that even without any knowledge of stochastic calculus and the corresponding Ito process one can approach the Black-Scholes option pricing PDE if one were to make the accommodation shown above. It also shows that any asset price movement, such as the movement of a bond, can be approximated by the Taylor series expansion and regardless of whether we know the exact closed form solution for the pricing of that asset, it is possible,

using first principles of differential calculus to approximate the movement of the asset over small increments of state space and time.

In keeping with our arguments above let us show you that the Taylor series expansion can be used to calculate the value of any variable with a great degree of precision and speed, which may not be possible numerically.

Say, you wanted to calculate the value of , that is eleven raised to the power of eight. Doing this manually could take you forever. Of course, you can do it in less than a second using a scientific calculator or an Excel spreadsheet. But suppose you don't have an Excel spreadsheet (or a calculator near you) and you wanted a quick approximation of this number.

You can say that and that a small increment of is one and therefore,
and . First we calculate the value of which is very
straightforward and simple: 100,000,000. We need to use the Taylor series to
calculate the change in value of this number around the point . (Remember
by making x = 10, we have made all our calculations very simple and that is where
the usefulness of Taylor series lies)

Now using Taylor series for calculation we get:

Thus the change in the value of the function f which is given by is:

And the value of the function is approximated as:

This is quite good an approximation given the fact that if you were to use your Excel spreadsheet then for 11^8 (eleven raised to the power of eight) you would get 214,358,881.

Math stuf is tuff to remember..

How many of you know what is a closed form expression? Here's what wikipedia tells me ( i'd have wasted a lot of time finding out math books if not for wikipedia..)..

"In mathematics, an equation or system of equations is said to have a closed-form solution if, and only if, at least one solution can be expressed analytically in terms of a bounded number of certain "well-known" functions. Typically, these well-known functions are defined to be elementary functions; so infinite series, limits, and continued fractions are not permitted.

For example, the roots of any quadratic equation with complex coefficients can be expressed in closed form in terms of addition, subtraction, multiplication, division, and square root extraction, all elementary functions. However, there are quintic equations without closed-form solutions using elementary functions — see Galois theory."

So, I'm reading up the steerable filter design for feature detection using canny-like criteria which claims to have a closed form solution to its filter design and not a fully computational approach . Got stumped by the first sentence itself and decided to look up on whats the closed form solution. Ok. now lemme proceed.

Here's another one. Whats the Taylor series expansion of an expression? ( deja vu???).. If you wanna approximate a function with the sum of the values of its derivatives at a point, you need the Taylor series . And if that point is x=0, then its called a McLauren series. Here's wiki to the rescue , yet again...

"The Taylor series is a representation of a function as an infinite sum of terms calculated from the values of its derivatives at a single point. It may be regarded as the limit of the Taylor polynomials. Taylor series are named in honour of English mathematician Brook Taylor. If the series uses the derivatives at zero, the series is also called a Maclaurin series, named after Scottish mathematician Colin Maclaurin."

• Have questions? Find out how to ask questions and get answers. •

As the degree of the Taylor series rises, it approaches the correct function. This image shows sinx and Taylor approximations,polynomialsof degree 1, 3, 5, 7, 9, 11 and 13.

complex function f that is infinitely differentiable in a neighbourhood of a real or complex number a, is the power series

which in a more compact form can be written

where n! is the factorial of n and f ⁽ⁿ⁾(a) denotes the nth derivative of f at the point a; the zeroth derivative of f is defined to be f itself and (x − a)⁰ and 0! are both defined to be 1.

THIS COULD BE USEFUL

The Maclaurin series for the exponential function e^x at a = 0 is