Interesting stuff.. how to approximately calculate 11^8 quickly without a calculator

You guessed it.. Taylor series...

HEre's the taylor series for f(x+ ) .
It is a simple expansion series of any function around a small increment .

Where are higher order terms (greater than the power of three). If we ignore
the higher order terms as well as the third order term then we can write:

And in the limiting case when we have

If you carefully look at the above equation then we will see a striking resemblance
to the famous Ito's stochastic equation, which is the basis of Black-Scholes option
pricing partial differential equation (PDE). The only difference is that in Ito's
equation we have the term instead of , that is in an Ito process we have

The above equivalence has a great intuitive meaning with respect of geometric Brownian motion and asset price movement, but that is not the purpose of this article. What we wanted to show was that even without any knowledge of stochastic calculus and the corresponding Ito process one can approach the Black-Scholes option pricing PDE if one were to make the accommodation shown above. It also shows that any asset price movement, such as the movement of a bond, can be approximated by the Taylor series expansion and regardless of whether we know the exact closed form solution for the pricing of that asset, it is possible,

using first principles of differential calculus to approximate the movement of the asset over small increments of state space and time.

In keeping with our arguments above let us show you that the Taylor series expansion can be used to calculate the value of any variable with a great degree of precision and speed, which may not be possible numerically.

Say, you wanted to calculate the value of , that is eleven raised to the power of eight. Doing this manually could take you forever. Of course, you can do it in less than a second using a scientific calculator or an Excel spreadsheet. But suppose you don't have an Excel spreadsheet (or a calculator near you) and you wanted a quick approximation of this number.

You can say that and that a small increment of is one and therefore,
and . First we calculate the value of which is very
straightforward and simple: 100,000,000. We need to use the Taylor series to
calculate the change in value of this number around the point . (Remember
by making x = 10, we have made all our calculations very simple and that is where
the usefulness of Taylor series lies)

Now using Taylor series for calculation we get:

Thus the change in the value of the function f which is given by is:

And the value of the function is approximated as:

This is quite good an approximation given the fact that if you were to use your Excel spreadsheet then for 11^8 (eleven raised to the power of eight) you would get 214,358,881.

Math stuf is tuff to remember..

How many of you know what is a closed form expression? Here's what wikipedia tells me ( i'd have wasted a lot of time finding out math books if not for wikipedia..)..

"In mathematics, an equation or system of equations is said to have a closed-form solution if, and only if, at least one solution can be expressed analytically in terms of a bounded number of certain "well-known" functions. Typically, these well-known functions are defined to be elementary functions; so infinite series, limits, and continued fractions are not permitted.

For example, the roots of any quadratic equation with complex coefficients can be expressed in closed form in terms of addition, subtraction, multiplication, division, and square root extraction, all elementary functions. However, there are quintic equations without closed-form solutions using elementary functions — see Galois theory."

So, I'm reading up the steerable filter design for feature detection using canny-like criteria which claims to have a closed form solution to its filter design and not a fully computational approach . Got stumped by the first sentence itself and decided to look up on whats the closed form solution. Ok. now lemme proceed.

Here's another one. Whats the Taylor series expansion of an expression? ( deja vu???).. If you wanna approximate a function with the sum of the values of its derivatives at a point, you need the Taylor series . And if that point is x=0, then its called a McLauren series. Here's wiki to the rescue , yet again...

"The Taylor series is a representation of a function as an infinite sum of terms calculated from the values of its derivatives at a single point. It may be regarded as the limit of the Taylor polynomials. Taylor series are named in honour of English mathematician Brook Taylor. If the series uses the derivatives at zero, the series is also called a Maclaurin series, named after Scottish mathematician Colin Maclaurin."

• Have questions? Find out how to ask questions and get answers. •

As the degree of the Taylor series rises, it approaches the correct function. This image shows sinx and Taylor approximations,polynomialsof degree 1, 3, 5, 7, 9, 11 and 13.

complex function f that is infinitely differentiable in a neighbourhood of a real or complex number a, is the power series

which in a more compact form can be written

where n! is the factorial of n and f ⁽ⁿ⁾(a) denotes the nth derivative of f at the point a; the zeroth derivative of f is defined to be f itself and (x − a)⁰ and 0! are both defined to be 1.

THIS COULD BE USEFUL

The Maclaurin series for the exponential function e^x at a = 0 is

Yuvraj..six sixes in an over..

Yuvraj!!!!!

Unsurprisingly, that's also the fastest Twenty20 fifty - it came up from 12 balls. Three fours, six sixes. More to the point, he's the first batsman to hit six sixes in Twenty20, and the fourth in senior cricket. Garry Sobers and Ravi Shastri did it in first-class matches, Herschelle Gibbs in the World Cup and now Yuvraj.
18.6
Broad to Yuvraj Singh, SIX, and he has, Yuvraj leans back and smacks that over wide mid-on ... it was the maximum from the moment it left that bat and the crowd were roaring as it flew
Broad looks quizzical ... and miserable. Can he ... can Yuvraj do it ... he looks like a man who knows he is about to be mauled again ...
18.5
Broad to Yuvraj Singh, SIX, down on one knee and larruped over midwicket, that one was more nine iron, it went into the night sky and dropped with a thud in the jubilant crowd ...
England have a team meeting. Shuffling deckchairs on the Jolly Roger though ...
18.4
Broad to Yuvraj Singh, SIX, Shiver me timbers!: Broad goes round the wicket, bowls a filthy wide full toss and Yuvraj steers it over backward point and it clears the rope again
18.3
Broad to Yuvraj Singh, SIX, he's hitting them everywhere, he steps to leg and smashes the ball over extra cover and it keeps on travelling ... the fireworks start on top of the scoreboard ... they've been going off in the middle for some time
18.2
Broad to Yuvraj Singh, SIX, now that really is sweet, no more than a dismissive flick off his legs, swatting a fly, and the ball arcs deep into the crowd beyond backward square leg
The dodgy TV measurement says that's 111 yards ... but as it landed outside the ground how the whatsists do they know? They guess, that's how.
18.1
Broad to Yuvraj Singh, SIX, that's out the ground, super shot over cow corner and it just kept going up

Computer Vision Basics -cameras

" Every man is ultimately a plagarist. How on earth can we call anything as an original creation?" -unknown

To understand computational cameras needed for optical vision, one needs to have a good solid technical foundation on some optical nuances, some of which are gonna be covered below. I have not written up anything which is below . They are just excerpts form internet or wikipedia.

Whats the "entrance pupil" ? An entrance pupil in optical systems is the area at the entry of the system which permits the entry of light into the system. It is a kind of an aperture. An aperture controls the amount of light entering the lens. For a camera a smaller aperture usually results in a larger field of view . This means that objects far away form it would be in focus. A larger aperture would require more expensive lenses and imaging stuff for good images. A larger aperture will have a lesser field of view. You can try that in your own camera by using an f/2.8 and f/32 aperture.

The amount of light captured by a lens is proportional to the area of the aperture, equal to:

Where f is focal length and N is the f number.

First on the list we need to know whats the f-number.
To put it in the easiest way, f-number is just simple: if the focal length is 5 times the diameter, the f-number is f/5.

Computer Vision Basics -

" The secret of creativity is not revealing the source." -Einstein

Photographic catadioptric lenses

500mm catadioptric lens mounted on a Yashica FX-3.

Photographic catadioptric lenses are similar to astronomical catadioptric designs and are used for some of the same reasons (with added modifications to accommodate photographic use). In order to make catadioptric "mirror lenses" less susceptible to blurring from internal air currents caused by external differential heating the internal space is sometimes filled with glass (referred to as a "solid-cat"). The refractive surfaces of the glass combined with added reflective (mirror) coatings are shaped to contribute to the optical properties of the whole mirror assembly, and so such devices are catadioptric. This has the added advantage of making them extremely rugged.

Catadioptric telescopes are designs that combine specifically shaped mirrors and lenses to allow very fast focal ratios (when used at the prime focus), while controlling coma and astigmatism.

Telescope makers also use catadioptric designs for any or all of the following reasons:

• They employ spherical surfaces that are easier to manufacture.
• When used in a cassegrain configuration it results in a long focal length instrument that is "folded" into a much smaller package.
• Catadioptric designs are low maintenance and rugged since some or all of their elements are fixed in alignment (collimation).
• Combining a moving primary mirror with a cassegrain configuration allow for large movements in the focal plane to accommodate cameras and CCDs.
• The corrector plates seal the tube assembly from dust and dirt. They also block air currents from the interior of the tube, thereby increasing image stability.

A disadvantage to this design is that the secondary mirror blocks a portion of the light entering the tube.

Light path in a Schmidt-Cassegrain

The Schmidt-Cassegrain is a classic wide-field telescope. The first optical element is a Schmidt corrector plate. The plate is figured by placing a vacuum on one side, and grinding the exact correction required to correct the spherical aberration caused by the primary mirror.

Thousands of amateur astronomers have purchased and used Schmidt-Cassegrain telescopes, with diameters from 20 cm (8 in.) to 48 cm (16 in.), since this type of telescope was introduced by Celestron in the 1960s. Now many companies mass-produce this type of telescope, at prices that make them quite affordable for many amateurs. One of the major advantages of the Schmidt-Cassegrain is that its folded light path makes the optical tube very short and squat, thus increasing its portability. It also has optics that are good for both planetary and deep sky observing.

Light path in a Maksutov-Cassegrain

The Maksutov-Cassegrain is a variation of the Maksutov telescope, invented by Dmitri Maksutov. It starts with an optically transparent corrector lens that is a section of a hollow sphere. It has a spherical primary mirror, and a spherical secondary that is often just a mirrored section of the corrector lens. Maksutovs are mechanically simpler than small Cassegrains, have a closed tube and all-spherical optics. The key difference from the similar Schmidt telescope design is the meniscus-shaped corrector plate, that has easy-to-make spherical surfaces, and not the complex aspherical form of the Schmidt design. Maksutovs tend to have a narrower field of view than Schmidt-Cassegrains due to their longer focal length and are generally heavier as well. However, their small secondary mirror gives them better resolution than a Schmidt-Cassegrain.

Irreducibility of polynomials - Interesting thought

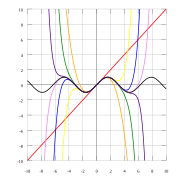
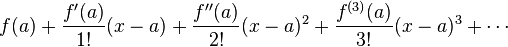Irreducibility CriteriaOne of the most well-known methods of determining whether a given
polynomial (with integer coefficients) is irreducible over the
rationals (meaning that it cannot be factored into smaller
polynomials with rational coefficients) is Eisenstein's criterion,
which states that if all the coefficients (except possibly the
first) are divisible by a prime p, and the constant coefficient
is *not* divisible by p^2, then the polynomial is irreducible.
It often happens that this criterion is not directly applicable
to a given polynomial f(x), but it may be applicable to f(x+a)
for some constant a. So we try various values of a, hoping to
transform f(x) into a polynomial that satisfies the conditions
of the criterion.
Notice that Eisenstein's criterion essentially reduces the problem
of factoring a polynomial of degree d to a problem of factoring d
integers, the coefficients of the transformed polynomial, to see if
they share a suitable common prime divisor. Obviously as we try
various transformations we will produce polynomials with larger and
larger coefficients, so the computational task of computing and then
checking the factorizations of those coefficients can be significant.
Moreover, a simple transformation that allows us to apply Eisenstein's
criterion may not even exist. However, if we are willing to factor
some large integers, there is another criterion that is, in some
ways, even easier than Eisenstein's, and that always works (assuming
the truth of a famous conjecture; see below).
Let F(x) denote a monic polynomial of degree d with integer
coefficients, and suppose we want to determine if this factors
into smaller polynomials with integer coefficients. If
F(x) = g(x)h(x) where g(x) and h(x) are non-constant polynomials
with integer coefficients then it follows that for any integer k
the number F(k) is divisible by the integers g(k) and h(k).
Now let's take the example F(x) = x^2 + 13*x + 11, and notice the
following values

F(-2) = -11
F( 0) = 11
F( 2) = 41
F( 8) = 179
F(10) = 241
These are each primes, so if F(k) = g(k)h(k) it follows that either
g(k) or h(k) is +-1 for each k = -2,0,2,8,19. Now, it's certainly
possible for one of these factor polynomials to give a value of +-1
for some argument k, but for how many different values of k is this
possible?
Clearly if d_g is the degree of g(x), then g(k) can equal +1 no more
than d_g times, because the polynomial g(x)-1 can have no more than
d_g roots. Similarly, g(k) can equal -1 for no more than d_g distinct
values of k. Thus, the maximum number of times that g(k) could equal
either +1 or -1 is 2(d_g), and by the same reasoning the max number of
times that h(k) could equal +-1 is 2(d_h). As a result, the maximum
possible number of distinct values of k for which F(k) can be a prime
(assuming F(x) factors as g(x)h(x)) is 2(d_g + d_h) = 2d. So, if
we can find 2d+1 distinct integers k such that F(k) is a prime (or a
unit), then F(x) is irreducible.
Furthermore, a "certificate of irreducibility" doesn't really need to
include all 2d+1 values of k. To understand why, suppose there are
distinct integers k1 and k2 such that g(k1)=1 and g(k2)=-1. Just to
illustrate, let's imagine that g(x) is of degree 3, so we have
(k1)^3 + A(k1)^2 + B(k1) + C = 1
(k2)^3 + A(k2)^2 + B(k2) + C = -1
Subtracting the second from the first gives
(k1^3 - k2^3) + A(k1^2 - k2^2) + B(k1 - k2) = 2
Notice that each term on the left is divisible by (k1-k2), so that
difference must be a divisor of the right hand side, which is 2. The
only integer divisors of 2 are +-1 and +-2, so if the numbers k1 and
k2 differ by more than 2, and if the absolute values of g(k1) and
g(k2) are both 1, then g(k1) and g(k2) must have the same sign.
Therefore, the maximum number of integers k differing by more than
2 for which g(k)=+-1 is only d_g, and the maximum number of such
integers for which h(k)=+-1 is only d_h, for a combined total of
(d_g + d_h) = d. Thus, if we can find d+1 integers k that differ
by more than 2 and such that F(k) is a prime or unit, then F(x) is
irreducible. For the preceeding example this means we can certify
the irreducibility with just the three values F(-2) = -11,
F( 2) = 41 , and F( 8) = 179.
Now, let's try this on a bigger polynomial, such as
F(x) = x^6 - 3x^5 - 87x^4 + 118x^3 - 33x^2 + 21x - 1
In this case we can easily compute
F(-22) = 107187629
F( -8) = -58601
F( -4) = -23269
F( 0) = -1
F( 12) = 634859
F( 18) = 19888469
F( 30) = 588786929
Each of the arguments -22, -8, .., 30 differs by more than 2 from the
others, and each of the 7 values of F(k) is a prime or a unit, so it
follows that F(x) is irreducible over the integers (and therefore
over the rationals).
Admittedly this requires us to test for primality of some fairly large
numbers F(k), but it's usually quite easy to detect composites, so
you can focus in quickly on a set of d+1 "probable primes", and then
rigorously prove primality. (Of course, the numbers in the above
example are small enough to simply check for trial divisors up to
the square root.) In comparison, Eisenstein's criterion would require
us to actually factor a large number of *sets* of coefficients of
transformed polynomials, looking for a set that is suitable, and with
no guarantee that a suitable one exists.
Of course, if F(x) actually IS reducible, then we will find that the
values of F(k) for all but at most 2d+1 values of k are composite. In
that case we can infer the polynomial factors of F(x) from the integer
factors of F(k), although it's probably easier to simply algebraically
solve the conditions on the coefficients of the factors.
One possible objection to the method of irreducibility testing described
above is thew fact that there exist irreducible polynomials f(x) such
that f(k) is *never* a prime for any integer k. However, the first
step in the method is really to construct a "primal polynomial" F(x)
whose factorability is the same as that of f(x). A primal polynomial
F(x) is one for which the greatest common divisor of all the values
F(k) is 1. If c is the constant coefficient of f(x) then the canonical
primal form of f(x) is F(x) = f(cx)/c. Clearly F(x) is irreducible if
and only if f(x) is irreducible (over the rationals).
For example, if f(x) = x^3 - 21x^2 + 98x + 6 we have c=6 and
the canonical primal form is
F(x) = f(6x)/6 = 36x^3 - 126x^2 + 98x + 1
which is irreducible in view of the values
F(-6) = -12899
F(-3) = -2399
F( 0) = 1
F( 9) = 16921
Notice that we have F(0)=1 by definition, so for a primal
polynomial of degree d we only need to find d non-trivial prime
values (with arguments differing from each other and 0 by more
than 2).
In fairness, I should mention that the assertion that this method
will *always* work is based on a famous unproved conjecture.
Specifically, in 1857 Bouniakowsky conjectured that if f(x) is
an irreducible polynomial with integer coefficients such that no
number greater than 1 divides all the values of f(k) for every
integer k, then f(k) is prime for infinitely many integers k.
On this basis, the above test for irreducibility will always
work. On the other hand, it won't always be easy. For example,
the first prime value of x^12 + 488669 occurs with x=616980 and
has 70 decimal digits.

Im back to blogging!

Today the 21st of August, 2007 was my first day at an MS class in Virginia Tech. WAs pretty interesting though. The pattern of life has changed a lot ever since ive been here. Normally i don't like speaking or even looking people on the face. And here at the Virginia Tech bookstore, I greet chinese, tamilians, arabs, americans and any TDH with a smile (made up of course!) and a very "homely" hello how r u greeting. And then a "Is there anything i could help you with?" query (my real nature tells me to shut up but... thats how the job is.. ).. But it's all fun.. being different and speaking to differen tpeople .. and its a whole different experience...in a space of a month.. from being in front of eclipse all the time to being a store vendor! .. a raeal difference it is...!!

Normally I'm very lazy to blog.. but today was kind of a day where I did nothing on the PC.. maybe i needed some space to do all kinds of friendly banter and ssquirt out all stupid stuffin my mind and let it wander into the vast wilderness of junk that it hits into.. (you'd be wondering..."what a yucky way of writing stuff!! " .. ) yaa i care hell about grammar and stuff.. who cares abt it in a blog.. this is not the next treatise on english literature.. is it??.. o blog.. i'll see you when i feel like doing this stuff again... till then take care.. nad sweet dreams!!