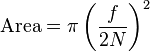Deals
Wednesday, September 19, 2007
Yuvraj..six sixes in an over..
Unsurprisingly, that's also the fastest Twenty20 fifty - it came up from 12 balls. Three fours, six sixes. More to the point, he's the first batsman to hit six sixes in Twenty20, and the fourth in senior cricket. Garry Sobers and Ravi Shastri did it in first-class matches, Herschelle Gibbs in the World Cup and now Yuvraj.
18.6
Broad to Yuvraj Singh, SIX, and he has, Yuvraj leans back and smacks that over wide mid-on ... it was the maximum from the moment it left that bat and the crowd were roaring as it flew
Broad looks quizzical ... and miserable. Can he ... can Yuvraj do it ... he looks like a man who knows he is about to be mauled again ...
18.5
Broad to Yuvraj Singh, SIX, down on one knee and larruped over midwicket, that one was more nine iron, it went into the night sky and dropped with a thud in the jubilant crowd ...
England have a team meeting. Shuffling deckchairs on the Jolly Roger though ...
18.4
Broad to Yuvraj Singh, SIX, Shiver me timbers!: Broad goes round the wicket, bowls a filthy wide full toss and Yuvraj steers it over backward point and it clears the rope again
18.3
Broad to Yuvraj Singh, SIX, he's hitting them everywhere, he steps to leg and smashes the ball over extra cover and it keeps on travelling ... the fireworks start on top of the scoreboard ... they've been going off in the middle for some time
18.2
Broad to Yuvraj Singh, SIX, now that really is sweet, no more than a dismissive flick off his legs, swatting a fly, and the ball arcs deep into the crowd beyond backward square leg
The dodgy TV measurement says that's 111 yards ... but as it landed outside the ground how the whatsists do they know? They guess, that's how.
18.1
Broad to Yuvraj Singh, SIX, that's out the ground, super shot over cow corner and it just kept going up
Tuesday, September 11, 2007
Computer Vision Basics -cameras
To understand computational cameras needed for optical vision, one needs to have a good solid technical foundation on some optical nuances, some of which are gonna be covered below. I have not written up anything which is below . They are just excerpts form internet or wikipedia.
Whats the "entrance pupil" ? An entrance pupil in optical systems is the area at the entry of the system which permits the entry of light into the system. It is a kind of an aperture. An aperture controls the amount of light entering the lens. For a camera a smaller aperture usually results in a larger field of view . This means that objects far away form it would be in focus. A larger aperture would require more expensive lenses and imaging stuff for good images. A larger aperture will have a lesser field of view. You can try that in your own camera by using an f/2.8 and f/32 aperture.
The amount of light captured by a lens is proportional to the area of the aperture, equal to:
Where f is focal length and N is the f number.
First on the list we need to know whats the f-number.
To put it in the easiest way, f-number is just simple: if the focal length is 5 times the diameter, the f-number is f/5.
Computer Vision Basics -
Photographic catadioptric lenses
Photographic catadioptric lenses are similar to astronomical catadioptric designs and are used for some of the same reasons (with added modifications to accommodate photographic use). In order to make catadioptric "mirror lenses" less susceptible to blurring from internal air currents caused by external differential heating the internal space is sometimes filled with glass (referred to as a "solid-cat"). The refractive surfaces of the glass combined with added reflective (mirror) coatings are shaped to contribute to the optical properties of the whole mirror assembly, and so such devices are catadioptric. This has the added advantage of making them extremely rugged.
Catadioptric telescopes are designs that combine specifically shaped mirrors and lenses to allow very fast focal ratios (when used at the prime focus), while controlling coma and astigmatism.Telescope makers also use catadioptric designs for any or all of the following reasons:
- They employ spherical surfaces that are easier to manufacture.
- When used in a cassegrain configuration it results in a long focal length instrument that is "folded" into a much smaller package.
- Catadioptric designs are low maintenance and rugged since some or all of their elements are fixed in alignment (collimation).
- Combining a moving primary mirror with a cassegrain configuration allow for large movements in the focal plane to accommodate cameras and CCDs.
- The corrector plates seal the tube assembly from dust and dirt. They also block air currents from the interior of the tube, thereby increasing image stability.
A disadvantage to this design is that the secondary mirror blocks a portion of the light entering the tube.
The Schmidt-Cassegrain is a classic wide-field telescope. The first optical element is a Schmidt corrector plate. The plate is figured by placing a vacuum on one side, and grinding the exact correction required to correct the spherical aberration caused by the primary mirror.Thousands of amateur astronomers have purchased and used Schmidt-Cassegrain telescopes, with diameters from 20 cm (8 in.) to 48 cm (16 in.), since this type of telescope was introduced by Celestron in the 1960s. Now many companies mass-produce this type of telescope, at prices that make them quite affordable for many amateurs. One of the major advantages of the Schmidt-Cassegrain is that its folded light path makes the optical tube very short and squat, thus increasing its portability. It also has optics that are good for both planetary and deep sky observing.
The Maksutov-Cassegrain is a variation of the Maksutov telescope, invented by Dmitri Maksutov. It starts with an optically transparent corrector lens that is a section of a hollow sphere. It has a spherical primary mirror, and a spherical secondary that is often just a mirrored section of the corrector lens. Maksutovs are mechanically simpler than small Cassegrains, have a closed tube and all-spherical optics. The key difference from the similar Schmidt telescope design is the meniscus-shaped corrector plate, that has easy-to-make spherical surfaces, and not the complex aspherical form of the Schmidt design. Maksutovs tend to have a narrower field of view than Schmidt-Cassegrains due to their longer focal length and are generally heavier as well. However, their small secondary mirror gives them better resolution than a Schmidt-Cassegrain.
Wednesday, September 05, 2007
Irreducibility of polynomials - Interesting thought
polynomial (with integer coefficients) is irreducible over the
rationals (meaning that it cannot be factored into smaller
polynomials with rational coefficients) is Eisenstein's criterion,
which states that if all the coefficients (except possibly the
first) are divisible by a prime p, and the constant coefficient
is *not* divisible by p^2, then the polynomial is irreducible.
It often happens that this criterion is not directly applicable
to a given polynomial f(x), but it may be applicable to f(x+a)
for some constant a. So we try various values of a, hoping to
transform f(x) into a polynomial that satisfies the conditions
of the criterion.
Notice that Eisenstein's criterion essentially reduces the problem
of factoring a polynomial of degree d to a problem of factoring d
integers, the coefficients of the transformed polynomial, to see if
they share a suitable common prime divisor. Obviously as we try
various transformations we will produce polynomials with larger and
larger coefficients, so the computational task of computing and then
checking the factorizations of those coefficients can be significant.
Moreover, a simple transformation that allows us to apply Eisenstein's
criterion may not even exist. However, if we are willing to factor
some large integers, there is another criterion that is, in some
ways, even easier than Eisenstein's, and that always works (assuming
the truth of a famous conjecture; see below).
Let F(x) denote a monic polynomial of degree d with integer
coefficients, and suppose we want to determine if this factors
into smaller polynomials with integer coefficients. If
F(x) = g(x)h(x) where g(x) and h(x) are non-constant polynomials
with integer coefficients then it follows that for any integer k
the number F(k) is divisible by the integers g(k) and h(k).
Now let's take the example F(x) = x^2 + 13*x + 11, and notice the
following values
F(-2) = -11
F( 0) = 11
F( 2) = 41
F( 8) = 179
F(10) = 241
These are each primes, so if F(k) = g(k)h(k) it follows that either
g(k) or h(k) is +-1 for each k = -2,0,2,8,19. Now, it's certainly
possible for one of these factor polynomials to give a value of +-1
for some argument k, but for how many different values of k is this
possible?
Clearly if d_g is the degree of g(x), then g(k) can equal +1 no more
than d_g times, because the polynomial g(x)-1 can have no more than
d_g roots. Similarly, g(k) can equal -1 for no more than d_g distinct
values of k. Thus, the maximum number of times that g(k) could equal
either +1 or -1 is 2(d_g), and by the same reasoning the max number of
times that h(k) could equal +-1 is 2(d_h). As a result, the maximum
possible number of distinct values of k for which F(k) can be a prime
(assuming F(x) factors as g(x)h(x)) is 2(d_g + d_h) = 2d. So, if
we can find 2d+1 distinct integers k such that F(k) is a prime (or a
unit), then F(x) is irreducible.
Furthermore, a "certificate of irreducibility" doesn't really need to
include all 2d+1 values of k. To understand why, suppose there are
distinct integers k1 and k2 such that g(k1)=1 and g(k2)=-1. Just to
illustrate, let's imagine that g(x) is of degree 3, so we have
(k1)^3 + A(k1)^2 + B(k1) + C = 1
(k2)^3 + A(k2)^2 + B(k2) + C = -1
Subtracting the second from the first gives
(k1^3 - k2^3) + A(k1^2 - k2^2) + B(k1 - k2) = 2
Notice that each term on the left is divisible by (k1-k2), so that
difference must be a divisor of the right hand side, which is 2. The
only integer divisors of 2 are +-1 and +-2, so if the numbers k1 and
k2 differ by more than 2, and if the absolute values of g(k1) and
g(k2) are both 1, then g(k1) and g(k2) must have the same sign.
Therefore, the maximum number of integers k differing by more than
2 for which g(k)=+-1 is only d_g, and the maximum number of such
integers for which h(k)=+-1 is only d_h, for a combined total of
(d_g + d_h) = d. Thus, if we can find d+1 integers k that differ
by more than 2 and such that F(k) is a prime or unit, then F(x) is
irreducible. For the preceeding example this means we can certify
the irreducibility with just the three values F(-2) = -11,
F( 2) = 41 , and F( 8) = 179.
Now, let's try this on a bigger polynomial, such as
F(x) = x^6 - 3x^5 - 87x^4 + 118x^3 - 33x^2 + 21x - 1
In this case we can easily compute
F(-22) = 107187629
F( -8) = -58601
F( -4) = -23269
F( 0) = -1
F( 12) = 634859
F( 18) = 19888469
F( 30) = 588786929
Each of the arguments -22, -8, .., 30 differs by more than 2 from the
others, and each of the 7 values of F(k) is a prime or a unit, so it
follows that F(x) is irreducible over the integers (and therefore
over the rationals).
Admittedly this requires us to test for primality of some fairly large
numbers F(k), but it's usually quite easy to detect composites, so
you can focus in quickly on a set of d+1 "probable primes", and then
rigorously prove primality. (Of course, the numbers in the above
example are small enough to simply check for trial divisors up to
the square root.) In comparison, Eisenstein's criterion would require
us to actually factor a large number of *sets* of coefficients of
transformed polynomials, looking for a set that is suitable, and with
no guarantee that a suitable one exists.
Of course, if F(x) actually IS reducible, then we will find that the
values of F(k) for all but at most 2d+1 values of k are composite. In
that case we can infer the polynomial factors of F(x) from the integer
factors of F(k), although it's probably easier to simply algebraically
solve the conditions on the coefficients of the factors.
One possible objection to the method of irreducibility testing described
above is thew fact that there exist irreducible polynomials f(x) such
that f(k) is *never* a prime for any integer k. However, the first
step in the method is really to construct a "primal polynomial" F(x)
whose factorability is the same as that of f(x). A primal polynomial
F(x) is one for which the greatest common divisor of all the values
F(k) is 1. If c is the constant coefficient of f(x) then the canonical
primal form of f(x) is F(x) = f(cx)/c. Clearly F(x) is irreducible if
and only if f(x) is irreducible (over the rationals).
For example, if f(x) = x^3 - 21x^2 + 98x + 6 we have c=6 and
the canonical primal form is
F(x) = f(6x)/6 = 36x^3 - 126x^2 + 98x + 1
which is irreducible in view of the values
F(-6) = -12899
F(-3) = -2399
F( 0) = 1
F( 9) = 16921
Notice that we have F(0)=1 by definition, so for a primal
polynomial of degree d we only need to find d non-trivial prime
values (with arguments differing from each other and 0 by more
than 2).
In fairness, I should mention that the assertion that this method
will *always* work is based on a famous unproved conjecture.
Specifically, in 1857 Bouniakowsky conjectured that if f(x) is
an irreducible polynomial with integer coefficients such that no
number greater than 1 divides all the values of f(k) for every
integer k, then f(k) is prime for infinitely many integers k.
On this basis, the above test for irreducibility will always
work. On the other hand, it won't always be easy. For example,
the first prime value of x^12 + 488669 occurs with x=616980 and
has 70 decimal digits.